I’ve always felt that mathematics is a useful tool in everyone’s daily life. Here is an example.
Recently, I was prescribed some medicine, and it was to be taken twice daily: once in the morning, and once before bed. However, I made a couple mistakes. The first morning, I took twice the dosage in the morning. And, in the evening I dutifully took another dosage, but made the same error and took a double dosage again. I realized my hapless error just as I downed the requisite glass of water. So what was I to do. Clearly, the drug was now above the prescribed concentration in my bloodstream, so should I continue the normal schedule the next morning?
We can use math to figure this out. Most drugs taken in orally can be considered to have a “half-life” in your bloodstream. Yes, this is the same concept of half-life in radioactivity. Basically, your body gets rid of stuff from your bloodstream at a constant rate, given the current concentration of the ‘stuff’ in your blood. This is modeled in math as an exponential decay function. To illustrate, have a look at these equations.

The simplest form is (1), which illustrates the basic shape of the drug concentration. We add a step function (2), which allows us to make just the part after the dose is administered, along with a t0 time offset parameter to give a more accurate shape in (3). (4) adds a half-life parameter, which is scaled away from the irrational e to become (5). This is the concentration resulting from a single dose, over all time, parameterized by dose administration (6). While you are taking the medicine (t=0 to t=t_finish), we can represent your idealized concentration as (7). The summation variable i gets incremented by 0.5 each time, which flies in the face of normal convention. Sorry about that. The code farther down is correct.
All simple, right? Let’s plot things. I used Mathematica to generate these plots. Equation (6) becomes:
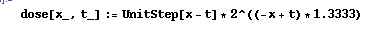
Note that in this function, x is time (in days), and t is the time offset. I threw the equation together before thinking about how best to represent things for others… Sorry…. The 1.3333 factor is the the half-life constant. The half-life for my medicine was roughly 18 hours, which is 0.75 days, which is roughly 1.3333 (close enough for my (government’s) purposes).
And then we can plot our ideal concentration.
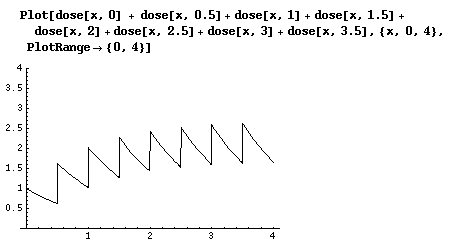
This is how the concentration would look like if I took the medicine exactly as directed. We can see that the concentration is roughly periodic after about two days of accumulation. But! I messed up, remember? How can I adjust my next doses to return to the ideal case?

You can see that at t=0, my medicine concentration is twice the ideal(conc = 2), since I took twice the dosage. Accordingly, the second dose, which was also twice too large, boosted my concentration to about 3.25. In this scenario, I skipped the third dosage (second day, morning), to bring my concentration roughly the same as the ideal case at t=1.5 . So there you go.
The bottom line is that I should skip the third dose if I take two double-doses on the first day. Yay! Isn’t math fun? This amount of math is no more than what a high-school graduate should have, and probably less than what an overachieving middle schooler could do.
I’ll be sure to post other examples math in real life when I get the gumption. Have a nice day!